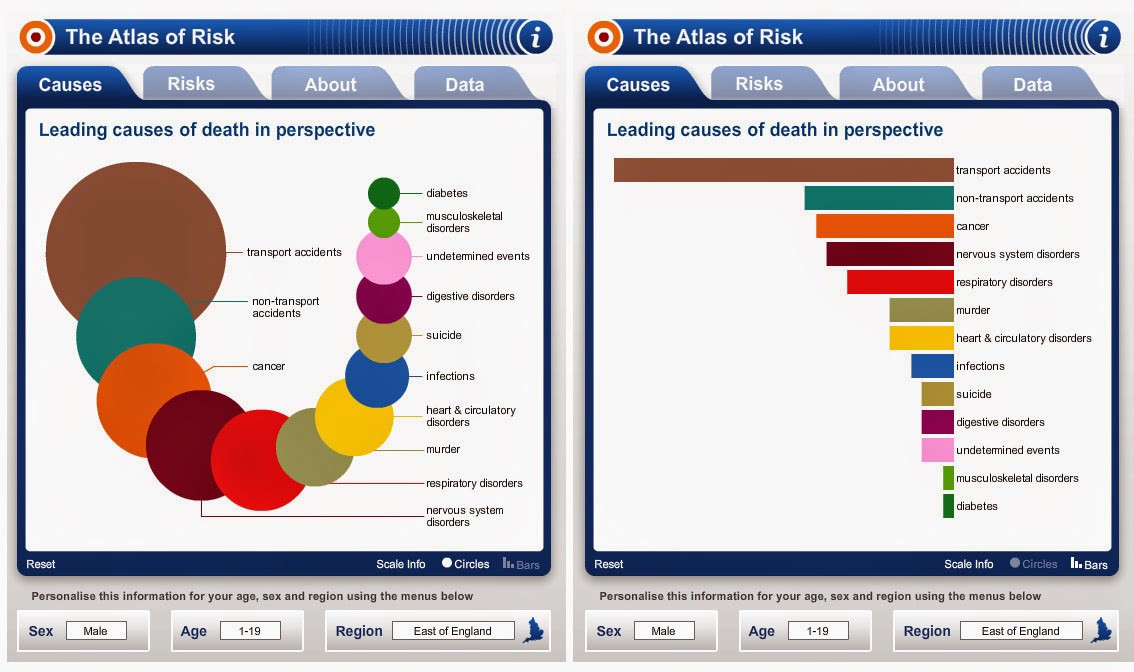
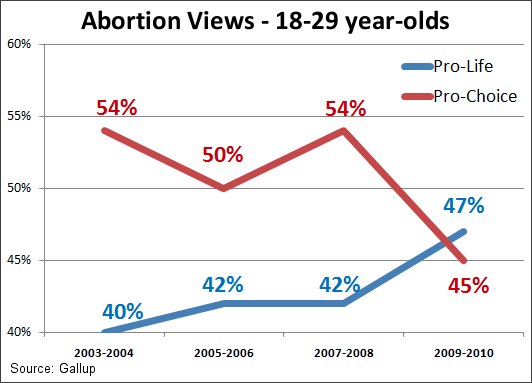
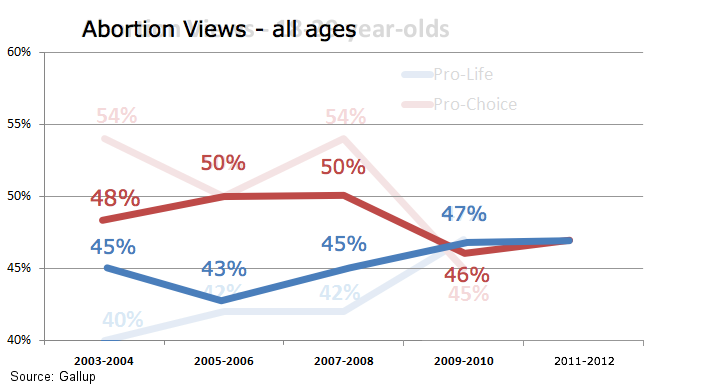
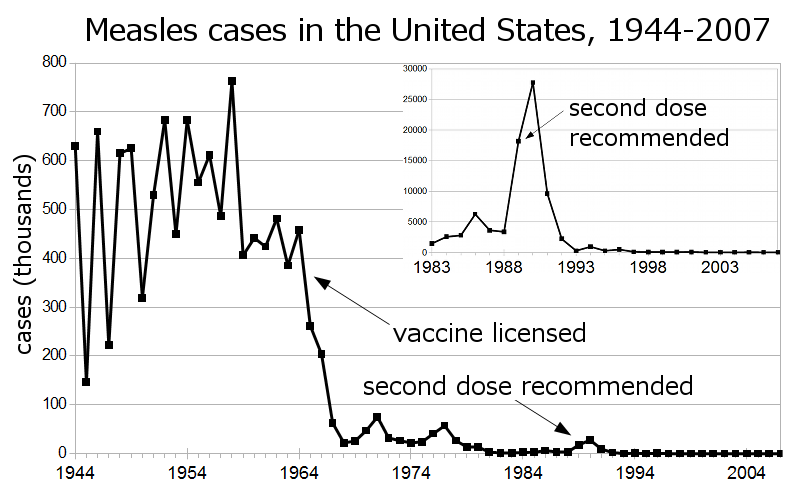
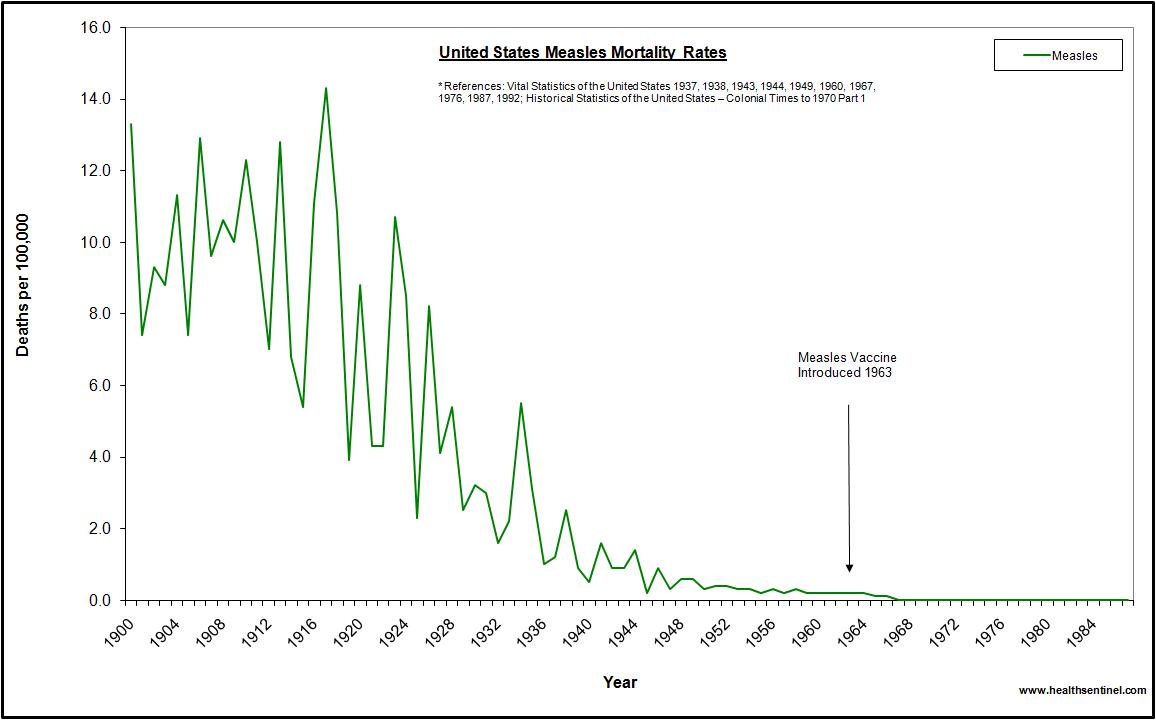
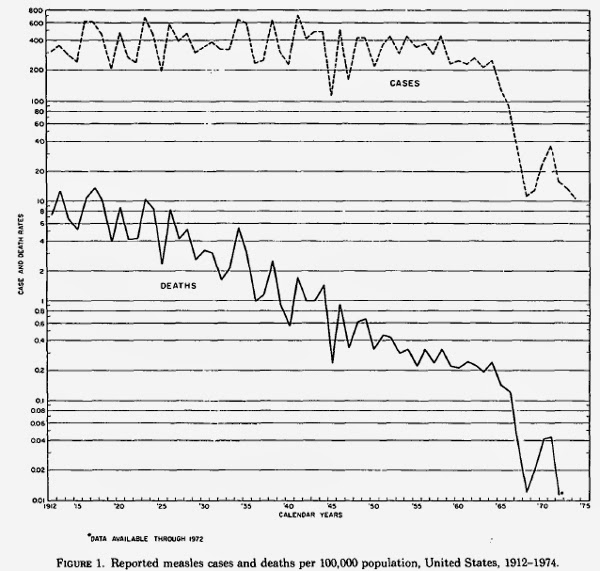
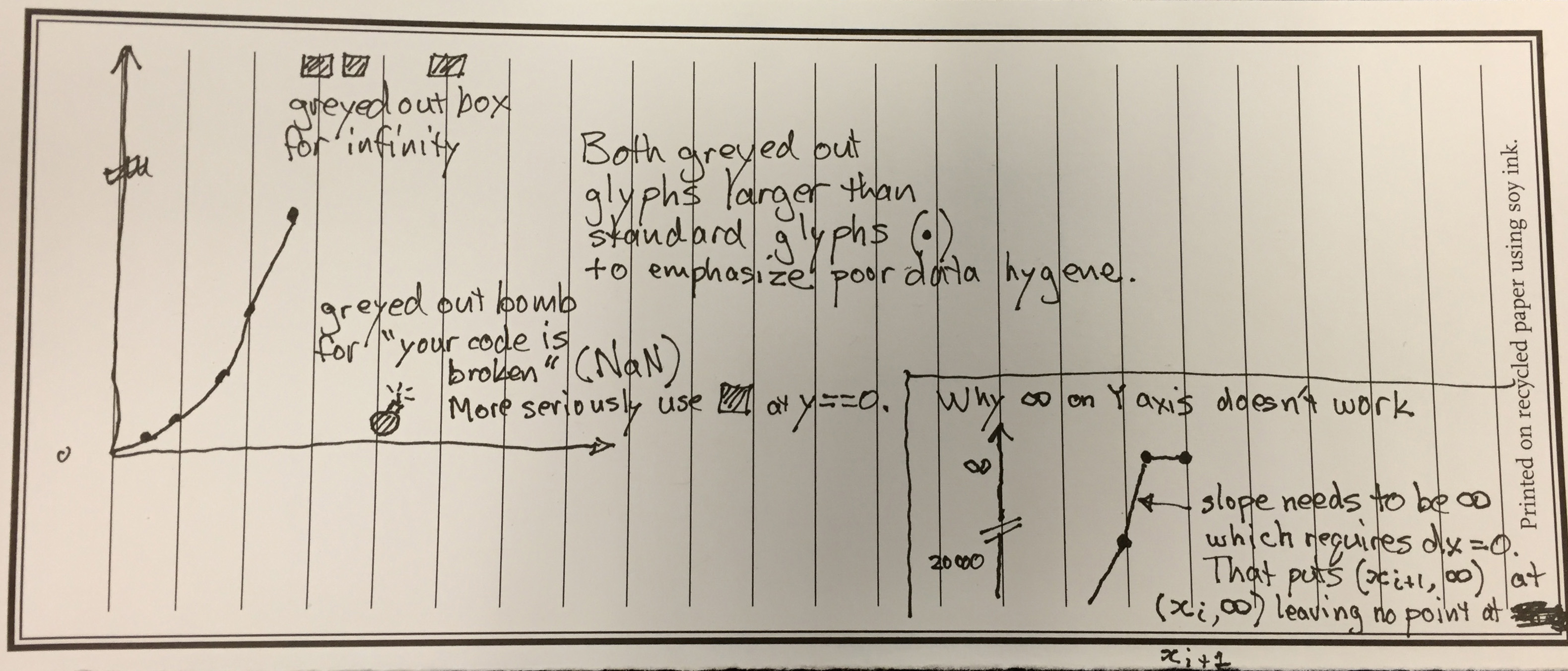
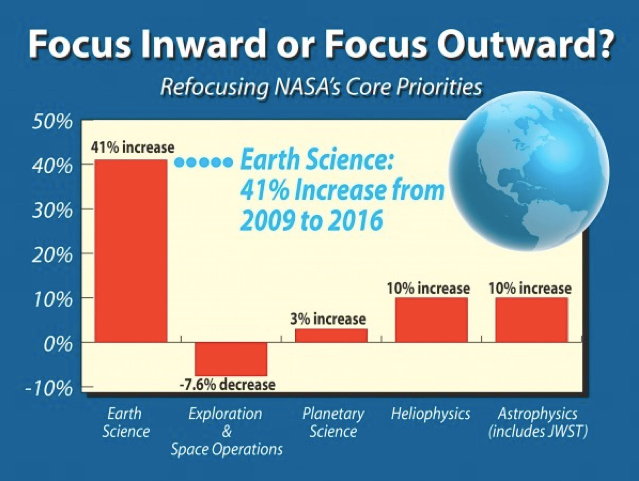
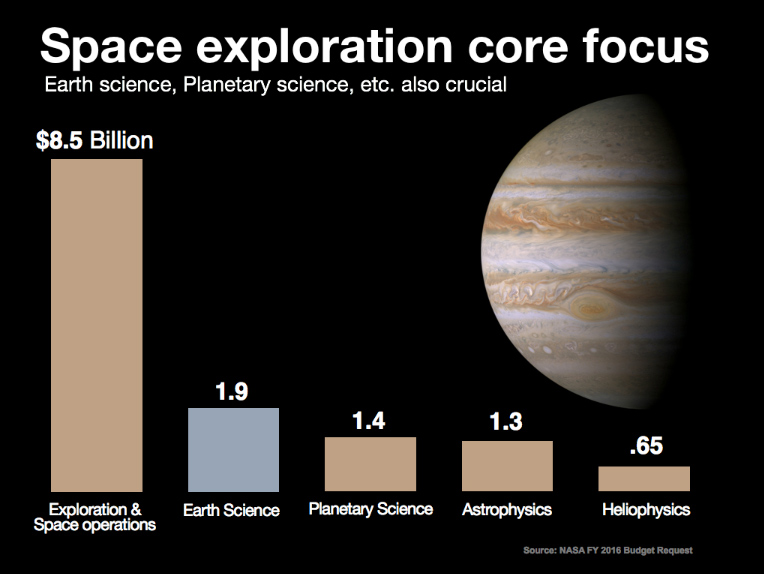
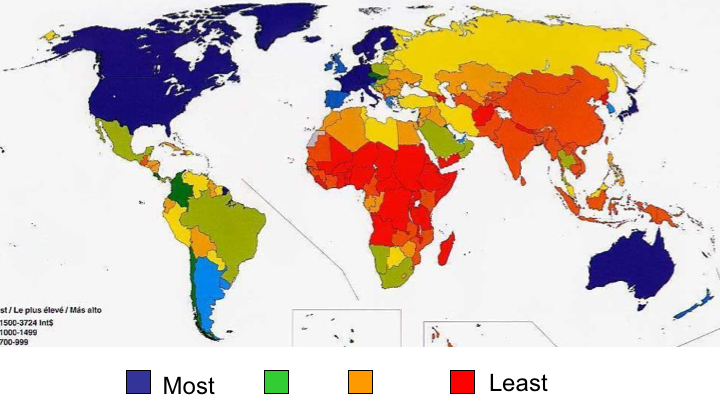
First we have this nice infographic on the different type of employers in Idaho. It shows bands with heights proportional to the percentage of employees in that category. To reinforce that it's in Idaho, the bands are embedded in the shape of Idaho.
And this is where we run into troubles. The shape of Idaho is quite irregular, which makes the relative size of the bands look different. Consider, for example, the third band from the top labeled “Trade, Transportation and Utilities.” At 20.2%, this is the tallest band on the map. But the region does not look very big because it happens to be located in the skinny panhandle. Areas like “Education and Health Services” and “Leisure and Hospitality” appear to be as larger even though their respective numbers are much smaller. And the bottom band, “Government,” appears to dwarf all other areas even though it is actually (supposed to be) smaller than “Trade, Transportation and Utilities.”